第6章 多组定量资料的比较
1. 多组样本均数比较的问题
为什么不能直接用 t 检验?
在比较三组或三组以上均数时,如果直接采用 t 检验进行两两比较,会带来严重的统计学问题:
- 过程繁琐:如果有 \(k\) 组样本,需要进行 \(k(k-1)/2\) 次比较。
- 误差估计不统一:每次 t 检验仅利用两组数据估计方差,没有利用所有数据,降低了检验的精确性和灵敏度。
- 犯 I 类错误(假阳性)概率累积增大:
- 设检验水准 \(\alpha=0.05\),每次不犯错误的概率为 \(0.95\)。
- 若比较4个组(需6次两两比较),整体不犯错误的概率为 \(0.95^6 \approx 0.735\)。
- 整体犯 I 类错误的概率(Family-wise Error Rate)飙升至 \(1 - 0.735 = 0.265\),远大于预设的 0.05。
因此,必须寻找一种能够同时检验多个均数是否相等的统计方法,即方差分析 (Analysis of Variance, ANOVA)。
例题:t检验两两比较的风险
对完全随机设计下的三个研究组均数进行比较时,若采用t检验两两比较,则主要( )。
A. 增大Ⅱ类错误概率
B. 增大Ⅰ类错误概率
C. 不会增大Ⅰ类错误概率
D. 不会增大Ⅱ类错误概率
E. 以上都不正确
正确答案: B
解析: 多次t检验未进行多重性校正时,整体Ⅰ类错误概率(假阳性率)会累积增大,远高于预设的显著性水平(如0.05)。
2. 方差分析的基本思想
核心原理:变异的分解
方差分析由英国统计学家 R.A. Fisher 首创。其核心思想是将所有观测值的总变异分解为不同的来源。
在完全随机设计(单因素方差分析)中,离均差平方和 (\(SS\)) 的分解如下: $$ SS_{总} = SS_{组间} + SS_{组内} $$
总变异 (\(SS_{总}\)):反映所有数据相对于总均数的离散程度。
组间变异 (\(SS_{组间}\)):反映处理效应(组间差异) + 随机误差。
组内变异 (\(SS_{组内}\)):仅反映随机误差(个体差异)。
均方与 F 值
均方 (MS):由平方和除以自由度得到,\(MS = SS / \nu\)。
注意:均方不具有可加性(即 \(MS_{总} \neq MS_{组间} + MS_{组内}\))。
F 值构造: $$ F = \frac{MS_{组间}}{MS_{组内}} $$ 判定:
若 \(H_0\) 成立(无处理效应),组间变异仅含随机误差,\(F \approx 1\)。
若 \(F\) 值显著大于 1(\(P < \alpha\)),说明组间变异显著大于组内变异,提示各组均数不全相等。
例题:变异分解公式
完全随机设计资料的方差分析中,必然有( )。
A. \(SS_{总} = SS_{组间} + SS_{组内}\)
B. \(MS_{总} = MS_{组间} + MS_{组内}\)
C. \(SS_{组间} > SS_{组内}\)
D. \(MS_{组间} > MS_{组内}\)
E. \(\nu_{总} > \nu_{组间} + \nu_{组内}\)
正确答案: A
解析: 在完全随机设计的方差分析中,总平方和(SS总)恒等于组间平方和(SS组间)与组内平方和(SS组内)之和,这是方差分析的基本分解原理。均方(MS)不具有可加性,自由度和平方和大小关系则不一定成立。
例题:组间均方的含义
完全随机设计资料的方差分析中,组间均方表示( )。
A. 抽样误差的大小
B. 处理效应的大小
C. 处理效应和抽样误差的综合结果
D. N个数据的离散程度
E. 随机因素的效应大小
正确答案: C
解析: 组间均方(MS组间)反映的是处理因素(组间差异)与随机误差的综合影响。若无处理效应,MS组间应接近MS组内(仅含误差);若存在处理效应,则MS组间会显著大于MS组内。
3. 实验设计的概念
方差分析的基础是正确识别实验设计类型。
三要素:
- 受试对象 (Object):动物、人体等。
- 处理因素 (Treatment):欲施加或观察的因素(如药物)。
- 实验效应 (Effect):处理因素作用的结果(指标)。
因素与水平:
因素 (Factor):引起效应的原因。
水平 (Level):因素在数量或强度上的不同取值。
方差分析类型:
单因素方差分析 (One-way ANOVA)
双因素方差分析 (Two-way ANOVA)
多因素方差分析 (N-way ANOVA)
4. 单因素方差分析 (One-way ANOVA)
完全随机设计
定义:将受试对象随机分配到各处理组。
假设检验:
无效假设 (\(H_0\)):各总体均数相等 (\(\mu_1 = \mu_2 = \dots = \mu_g\))。
备择假设 (\(H_1\)):各总体均数不全相等(至少有一对不等)。
与 t 检验的关系:
当组数 \(g=2\) 时,方差分析与 t 检验等价,且 \(F = t^2\)。
例题:统计推断结论
若单因素方差分析结果为 \(F>F_{0.05}(\nu_1,\nu_2)\),则统计推断是( )。
A. 各样本均数都不相等
B. 各样本均数不全相等
C. 各总体均数都不相等
D. 各总体均数不全相等
E. 各总体均数全相等
正确答案: D
解析: 方差分析的原假设是“各总体均数相等”,拒绝原假设时的结论应为“各总体均数不全相等”,即至少有两个总体均数不同,而非全部不同。
例题:两组比较的方法
定量资料两样本均数的比较,可采用( )。
A. t检验
B. F检验
C. Bonferroni检验
D. t检验与F检验均可
E. LSD检验
正确答案: D
解析: 两样本均数比较通常用 t 检验,但方差分析(F检验)也可用于两组比较,且结果一致。
例题:F检验与t检验的关系
当组数等于2时,对于同一资料,方差分析结果与t检验结果相比,( )。
A. t检验结果更为准确
B. 方差分析结果更为准确
C. 完全等价且 \(F=t^2\)
D. 完全等价且 \(F=\sqrt{t}\)
E. 两者结果可能出现矛盾
正确答案: C
解析: 在两组比较时,方差分析的F统计量等于t检验统计量的平方,即 \(F=t^2\),因此两者完全等价,结论一致。
随机区组设计 (Randomized Block Design)

原理:先将受试对象按非处理因素(如体重、性别)配成区组 (Block),使区组内性质尽可能一致,区组间差异尽可能大,再将区组内对象随机分配到各处理组。
优势:随机区组设计确定区组的因素应是对试验结果有影响的非处理因素。区组内各试验对象应均衡,区组之间试验对象具有较大的差异为好,这样就可以利用区组控制非处理因素的影响,并在方差分析时将区组间的变异从组内变异中分解出来。当区组间差别有统计学意义时,这种设计的误差比完全随机设计小,试验效率得以提高。
变异分解:
\(\(SS_{总} = SS_{处理} + SS_{区组} + SS_{误差}\)\)
例子

处理方法:将区组作为另一个处理因素
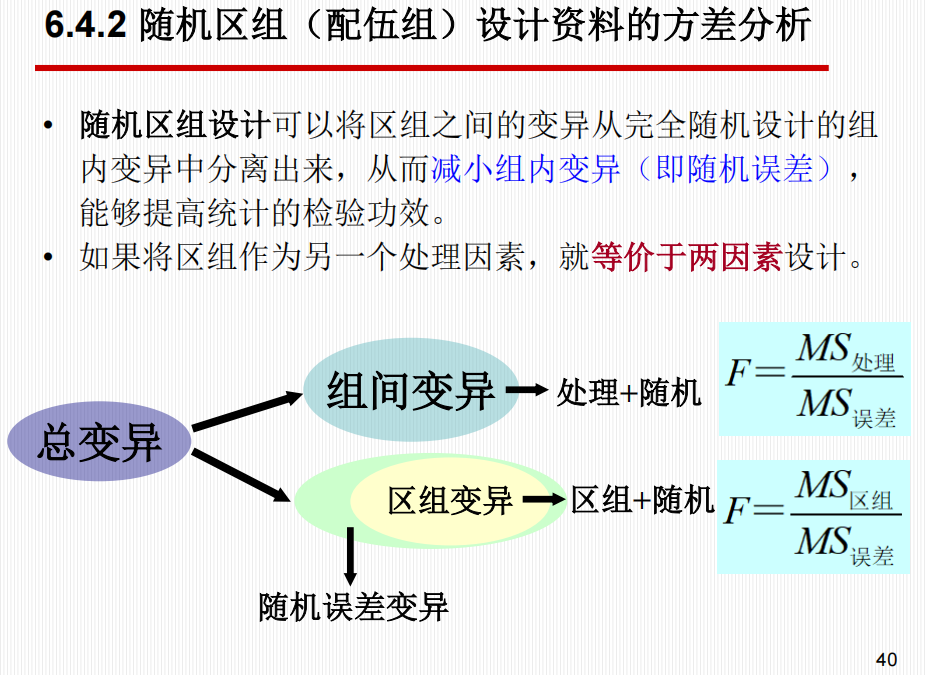
例题:随机区组变异分解
10. 随机区组设计资料的方差分析中,以下正确的是( )。
A. \(SS_{总} = SS_{组间} + SS_{组内}\)
B. \(SS_{总} = SS_{处理} + SS_{误差}\)
C. \(SS_{总} = SS_{处理} + SS_{区组} + MS_{误差}\)
D. \(MS_{总} = MS_{组间} + MS_{组内}\)
E. \(MS_{总} = MS_{组间} + MS_{区组} + MS_{组内}\)
正确答案: A (注:此题选项A在部分教材中指代One-way ANOVA的分解。但在随机区组语境下,最准确的描述应是 \(SS_{总} = SS_{处理} + SS_{区组} + SS_{误差}\)。若必须选A,通常是因为将“组内”理解为包含了区组和误差的剩余部分,但C/D/E明显错误)
拉丁方设计
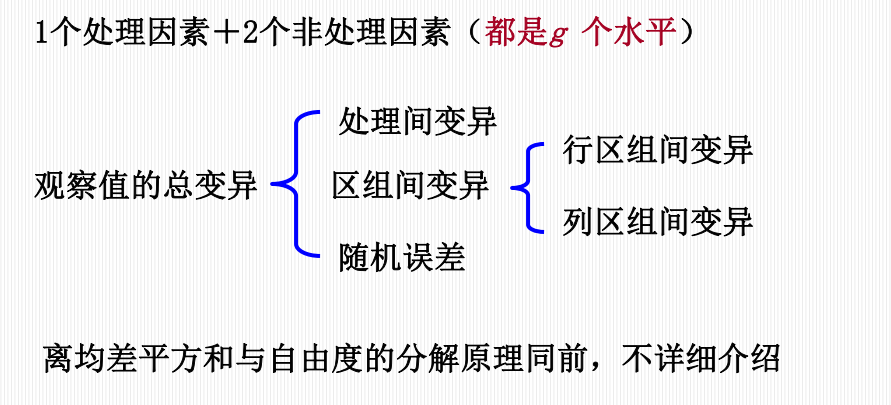
结构:1个处理因素 + 2个非处理因素(行区组、列区组),且都为 \(g\) 个水平。
变异分解:\(SS_{总} = SS_{处理} + SS_{行区组} + SS_{列区组} + SS_{误差}\)。
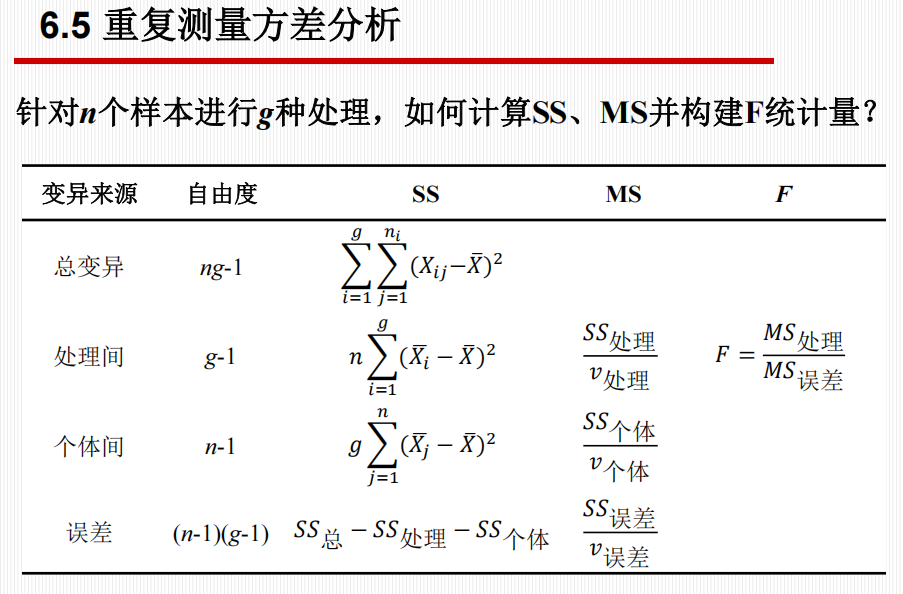
5.重复测量方差分析 (Repeated Measures ANOVA)
定义:对同一组个体或样本在不同时间点或不同处理条件下进行多次测量。
数据特点:数据来自于非独立样本(Dependent sample),类似于配对 t 检验的扩展。
变异分解:
由于每个个体在所有条件下都贡献了数据,个体间的差异可以分离出来:
$$
SS_{总} = SS_{处理} + SS_{个体} + SS_{误差}
$$
优势:
- 减少个体差异的影响,提高统计效率。
- 节省样本量。
6.多个均数间的两两比较 (Post-hoc Tests)
当方差分析结果显示“均数不全相等”(拒绝 \(H_0\))时,需进一步进行两两比较。
LSD-t 检验 (最小显著差异法)
实质是 t 检验,但采用统一的误差 (\(MS_{误差}\)) 和自由度。
灵敏度最高,但容易犯 I 类错误。
Bonferroni 法
原理:调整检验水准 \(\alpha' = \alpha / m\) (\(m\) 为比较次数)。
严格控制总体 I 类错误,但结论偏保守,容易犯 II 类错误。
FDR (False Discovery Rate, 假发现率)
核心思想:控制错误发现(假阳性)的比例,而非完全避免。
Benjamini-Hochberg (B-H) 算法
对 P 值排序,寻找阈值,适合高维数据(如基因数据)。
例题:多重比较方法辨析
以下说法正确的是( )。
A. 多个样本均数之间的两两比较,方法有LSD-t检验法,Bonferroni法,FDR法。
B. LSD-t检验实质上就是t检验,只是采用了统一的误差,结论偏于保守。
C. Bonferroni法在比较次数过多时,由于检验水准调整过低,结论偏于保守。
D. FDR是假发现率,它的核心思想是在进行多次假设检验时,允许一定比例的错误发现(即虚假阳性),以提高整体的统计效率。
E. 当比较20000个基因数据时,使用Bonferroni法可以灵敏检测出一些高表达的基因。
正确答案: A C D
解析: A正确。B错误,LSD法并未严格控制I类错误,实际上偏于“不保守”(容易发现差异)。C正确,Bonferroni法非常严格。D正确,FDR适合高维数据。E错误,Bonferroni在比较次数巨大时(如20000次)太保守,会导致大量假阴性(漏诊),不灵敏。
7. 方差分析的应用条件与检验
三大前提
- 独立性:各样本是相互独立的随机样本。
- 正态性:各样本来自正态分布——正态性检验
- 方差齐性 (Homogeneity of Variance):各总体方差相等——方差齐性检验
检验方法
方差齐性检验
Bartlett 检验:对正态性敏感。
Levene 检验:稳健,不严格依赖正态分布,目前最常用。
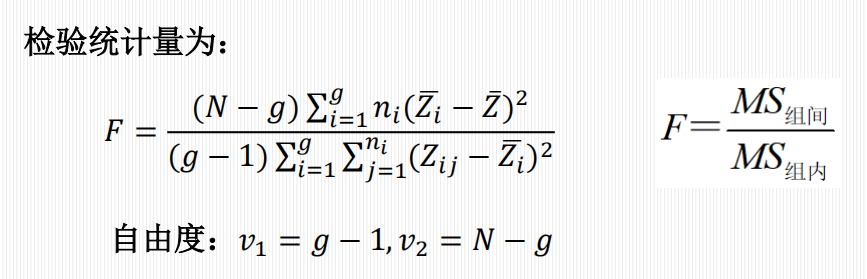
检验假设:\(H_0\) 为各总体方差相等。\(H_1\) 为各总体方差不全相等。
残差图 (Residual Plot)
若散点随机分布在0轴上下,无明显趋势,则满足正态性和方差齐性。
数据变换
若不满足条件,可尝试数据变换(对数、平方根、反正弦变换)。
例题:方差齐性检验结论
k个方差齐性检验有统计学意义,可认为( )。
A. \(\sigma_1^2, \sigma_2^2, \dots, \sigma_k^2\) 不全相等
B. \(\mu_1, \mu_2, \dots, \mu_k\) 不全相等
C. \(S_1, S_2, \dots, S_k\) 不全相等
D. \(\bar{X}_1, \bar{X}_2, \dots, \bar{X}_k\) 不全相等
E. \(\sigma_1^2, \sigma_2^2, \dots, \sigma_k^2\) 全不相等
正确答案: A
解析: 方差齐性检验的原假设是各总体方差相等。若检验有统计学意义(P < 0.05),则拒绝原假设,认为总体方差不全相等。
8. 非参数检验 (Kruskal-Wallis 检验)
当多组数据不满足方差分析条件(非正态或方差不齐)时,应使用非参数检验。
方法:Kruskal-Wallis H 检验(多组独立样本的秩和检验)。
假设:
\(H_0\):各总体分布相同。
\(H_1\):各总体分布不全相同。
步骤:混合编秩,求各组秩和 \(R_i\),计算统计量 \(H\)。
相同秩次 (Ties) 的影响: 若存在相同数值(结),需使用平均秩次。若不进行校正,计算出的 \(H\) 值会偏小,导致 \(P\) 值偏大(保守),降低检验效能。
例题:非参数检验的选择
多样本定量资料比较,当分布类型不清时应选择( )。
A. 方差分析
B. t检验
C. Z检验
D. Kruskal-Wallis检验
E. Wilcoxon检验
正确答案: D
解析: Kruskal-Wallis检验是非参数方法,适用于多个独立样本在总体分布未知或非正态时的比较。Wilcoxon检验通常用于两样本。
例题:相同秩次的影响
多组样本比较的Kruskal-Wallis检验中,当相同秩次较多时,如果用H值而不校正后的Hc值,则会( )。
A. 提高检验的灵敏度
B. 把一些无差别的总体推断成有差别
C. 把一些有差别的总体推断成无差别
D. Ⅰ、Ⅱ类错误概率不变
E. 以上说法均不对
正确答案: C
解析: 当存在较多结(相同秩次)时,未校正的 H 值会低估真实检验统计量,导致 P 值偏大,从而可能无法拒绝实际上应拒绝的原假设。这意味着降低了检验效能,容易犯 II 类错误(把有差别的误判为无差别)。
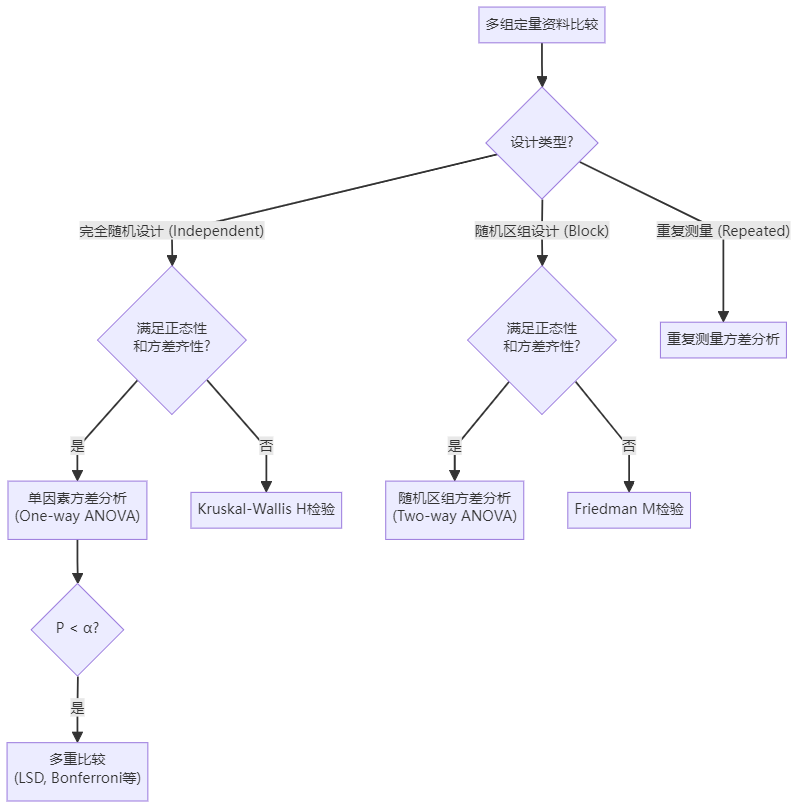
8. 多组定量资料比较流程图