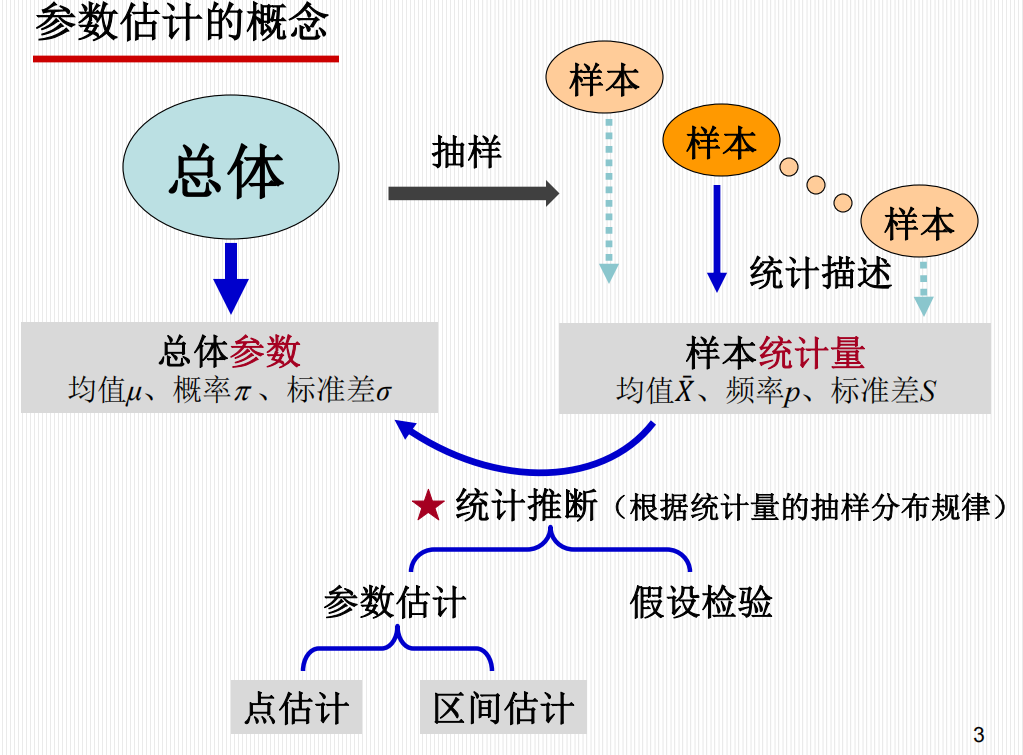
第3章 参数估计
1. 概述
统计推断 (Statistical Inference)
统计推断是指根据统计量的抽样分布规律,由样本统计量推断总体参数的过程。它包含两个核心内容:
参数估计 (Parameter Estimation):推断总体的数量特征(如均数、概率)。
假设检验 (Hypothesis Testing):对总体的某种假设进行检验。
总体与样本的指标
总体参数:描述总体特征的指标,如总体均值 \(\mu\)、总体概率 \(\pi\)、总体标准差 \(\sigma\)。
样本统计量:描述样本特征的指标,如样本均值 \(\bar{X}\)、样本频率 \(p\)、样本标准差 \(S\)。
2.抽样分布与标准误
抽样分布 (Sampling Distribution)
从同一总体中,随机抽取相同含量的样本,由重复抽取的每一份样本可以计算获得每一个样本统计量(如样本均数)。
这些样本统计量(如 \(m\) 个样本均数)构成的分布称为样本均数的抽样分布。
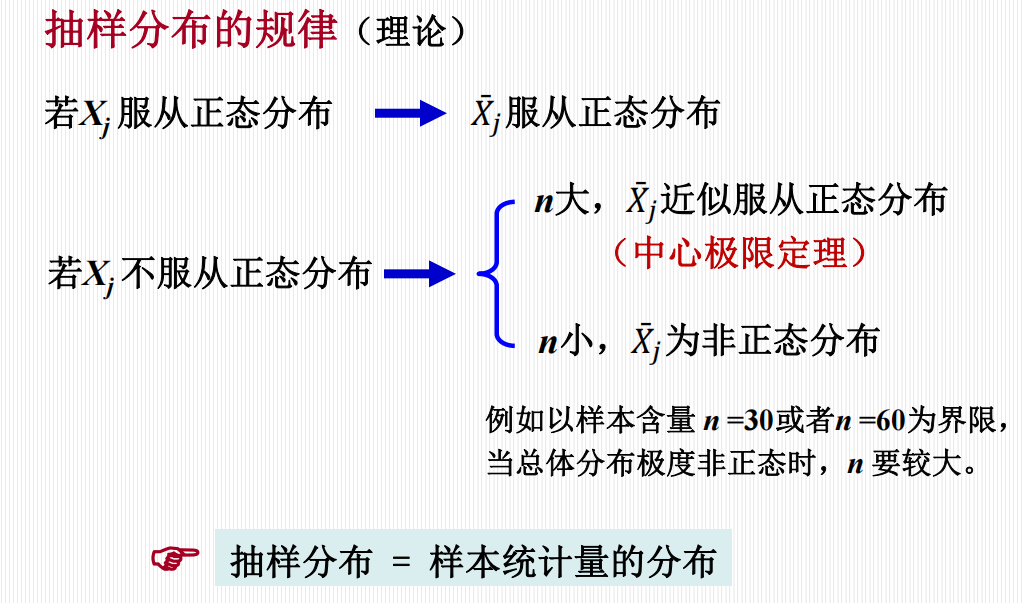
样本均数的抽样分布
中心极限定理:当有足够的样本含量时,从任何总体中抽取随机样本的样本均数近似地服从正态分布。
分布特点:
各样本均数不一定等于总体均数。
各样本均数间存在差异。
分布中间多,两边少,左右基本对称。
变异范围较之原变量的变异范围大大缩小。
标准误 (Standard Error, SE):
样本统计量的标准差,表示抽样误差大小的统计指标。
均数标准误计算公式:
\(\sigma_{\bar{X}} = \frac{\sigma}{\sqrt{n}}\)
若总体标准差未知,用样本标准差 \(S\) 估计:
\(S_{\bar{X}} = \frac{S}{\sqrt{n}}\)
例题:标准误的意义
( )小,表示用样本均数估计总体均数的精确度高。
A. CV
B. S
C. \(S_{\bar{X}}\)
D. R
E. 四分位数间距
正确答案: C
解析: \(S_{\bar{X}}\) 即均数的标准误,反映样本均数与总体均数的离散程度(抽样误差),值越小说明估计越精确。
两个样本均数之差的抽样分布
情形一:总体方差已知
若两个总体服从正态分布 \(X_1 \sim N(\mu_1, \sigma_1^2)\) 和 \(X_2 \sim N(\mu_2, \sigma_2^2)\),则两个样本均数之差 \(\bar{X}_1 - \bar{X}_2\) 也服从正态分布。
均数:\(\mu_{\bar{X}_1 - \bar{X}_2} = \mu_1 - \mu_2\)
标准误:
\(\sigma_{\bar{X}_1 - \bar{X}_2} = \sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}}\)
情形二:总体方差未知
用样本方差估算标准误。
若方差不等 (\(\sigma_1^2 \neq \sigma_2^2\)):
\(S_{\bar{X}_1 - \bar{X}_2} = \sqrt{\frac{S_1^2}{n_1} + \frac{S_2^2}{n_2}}\)
若方差相等 (\(\sigma_1^2 = \sigma_2^2\)):
需先计算合并标准差 \(S_c\):
\(S_c = \sqrt{\frac{(n_1-1)S_1^2 + (n_2-1)S_2^2}{(n_1-1) + (n_2-1)}}\)
此时标准误为:
\(S_{\bar{X}_1 - \bar{X}_2} = S_c \sqrt{\frac{1}{n_1} + \frac{1}{n_2}}\)
样本频率的抽样分布
分布规律:
若总体成功概率为 \(\pi\),样本成功频率为 \(p = X/n\)。
当 \(n\) 足够大时,\(p\) 的抽样分布接近正态分布。
均数:\(\mu_p = \pi\)
标准误:
理论值:\(\sigma_p = \sqrt{\frac{\pi(1-\pi)}{n}}\)
估计值(\(\pi\) 未知时):\(S_p = \sqrt{\frac{p(1-p)}{n}}\)
例题:频率的标准误
样本频率与总体概率均已知时,计算样本频率的抽样误差的公式为( )。
A. \(\sqrt{\frac{p(1-p)}{n}}\)
B. \(\sqrt{\frac{p(1-p)}{n-1}}\)
C. \(\sqrt{\frac{\pi(1-\pi)}{n}}\)
D. \(\sqrt{\frac{\pi(1-\pi)}{n-1}}\)
E. \(\sqrt{\frac{\pi(1-\pi)}{n-2}}\)
正确答案: C
解析: 样本频率的抽样误差即标准误。若总体概率 \(\pi\) 已知,应使用理论公式 \(\sigma_p = \sqrt{\frac{\pi(1-\pi)}{n}}\)。
两个样本频率之差的抽样分布
对于两个二项分布样本频率差值 \(p_1 - p_2\)。
均数:\(\mu_{p_1 - p_2} = \pi_1 - \pi_2\)
标准误:
一般情况 (\(\pi_1 \neq \pi_2\)):
\(S_{p_1 - p_2} = \sqrt{\frac{p_1(1-p_1)}{n_1} + \frac{p_2(1-p_2)}{n_2}}\)
3.Z分布与t分布
Z分布 (标准正态分布)
如果随机变量 \(X\) 服从正态分布 \(N(\mu, \sigma^2)\),则 \(Z = \frac{X - \mu}{\sigma}\) 服从标准正态分布 \(N(0, 1)\)。
对于样本均数:\(\frac{\bar{X} - \mu}{\sigma/\sqrt{n}} \sim Z\)。
t分布
当总体标准差 \(\sigma\) 未知时,用样本标准差 \(S\) 代替 \(\sigma\),此时统计量服从 \(t\) 分布:
\(\frac{\bar{X} - \mu}{S/\sqrt{n}} \sim t(\nu)\),其中 \(\nu = n-1\) 为自由度。
图形特征:
单峰分布,以0为中心,左右对称。
自由度 \(\nu\) 越小,峰部越矮,尾部越高(数据越分散)。
当 \(\nu \to \infty\) 时,\(t\) 分布逼近 \(Z\) 分布(标准正态分布)。
例题:t分布的特征
关于以0为中心的t分布,错误的是( )。
A. t分布的概率密度图是一簇曲线
B. t分布的概率密度图是单峰分布
C. 当 \(\nu \to \infty\) 时,t分布 \(\to\) z分布
D. t分布的概率密度图以0为中心,左右对称
E. \(\nu\) 相同时,\(|t|\) 值越大,P值越大
正确答案: E
解析: t分布是单峰对称的。\(|t|\) 值越大,越靠近尾部,对应的尾部面积(概率P值)越小。
4.总体参数的估计
估计类型
点估计 (Point Estimation):用样本统计量直接作为总体参数的估计值(如用 \(\bar{X}\) 估计 \(\mu\))。缺点是无法反映抽样误差。
区间估计 (Interval Estimation):结合样本统计量及其标准误,确定一个包含总体参数的区间(置信区间 CI)。
总体均数的置信区间
Z分布法:
适用条件:总体标准差 \(\sigma\) 已知,或样本量较大 (\(n>30\))。
双侧置信区间公式:
\(\bar{X} \pm Z_{\alpha/2} \sigma_{\bar{X}}\)
(若 \(\sigma\) 未知且 \(n\) 较大,可用 \(S_{\bar{X}}\) 近似)
t分布法:
适用条件:总体标准差 \(\sigma\) 未知,且 \(n\) 较小,数据服从正态分布。
双侧置信区间公式:
\(\bar{X} \pm t_{\alpha/2, \nu} S_{\bar{X}}\)
例题:均数的抽样误差
在已知均数为 \(\mu\),标准差为 \(\sigma\) 的正态总体中随机抽样, \(|\bar{X}-\mu| > (\quad)\) 的概率为5%。
A. \(1.96\sigma\)
B. \(1.96\sigma_{\bar{X}}\)
C. \(t_{0.05/2, \nu}S\)
D. \(t_{0.05/2, \nu}S_{\bar{X}}\)
E. \(U_{0.05/2}\sigma\)
正确答案: B
解析: 95%的样本均数落在 \(\mu \pm 1.96\sigma_{\bar{X}}\) 范围内,因此落在该范围外的概率为5%。
两总体均数之差的置信区间
公式:
\((\bar{X}_1 - \bar{X}_2) \pm t_{\alpha/2, \nu} S_{\bar{X}_1 - \bar{X}_2}\)
自由度 \(\nu\):
若 \(\sigma_1^2 \neq \sigma_2^2\):使用 Satterthwaite 近似公式计算 \(\nu\)。
若 \(\sigma_1^2 = \sigma_2^2\):\(\nu = n_1 + n_2 - 2\)。
总体概率的置信区间
查表法:适用于 \(n \le 50\)。
正态近似法:
适用条件:\(n\) 较大 (\(>50\)),且 \(np\) 和 \(n(1-p)\) 均大于 5。
公式:
\(p \pm Z_{\alpha/2} S_p\)
其中 \(S_p = \sqrt{\frac{p(1-p)}{n}}\)
两总体概率之差的置信区间
适用条件:\(n_1, n_2\) 较大,且 \(n_1 p_1, n_1(1-p_1)\) 等均大于 5。
公式:
\((p_1 - p_2) \pm Z_{\alpha/2} S_{p_1 - p_2}\)
其中 \(S_{p_1 - p_2} = \sqrt{\frac{p_1(1-p_1)}{n_1} + \frac{p_2(1-p_2)}{n_2}}\)
置信区间的准确度和精确度
1.置信度(1-α)越大,~1,准确度越高,但不一定有用
2.精确度是置信区间的半宽度,越窄越好
3.抽样误差(标准误)一定时,准确度与精确度两者不可兼顾
4.增加样本含量n,可以降低抽样误差,从而提高参数估计的精确度
5.应用举例与辨析
置信区间vs参考值范围
| 维度 | 置信区间 (CI) | 参考值范围 (Reference Range) |
|---|---|---|
| 含义 | 估计总体参数(如总体均数)的波动范围 | 估计个体值(如大多数正常人)的波动范围 |
| 用途 | 统计推断,估计参数 | 统计描述,辅助诊断判断个体是否正常 |
| 计算依据 | 使用标准误 (\(S_{\bar{X}}\)) | 使用标准差 (\(S\)) |
| 公式(正态) | \(\bar{X} \pm t_{\alpha/2} S_{\bar{X}}\) | \(\bar{X} \pm 1.96S\) (95%) |
| 宽度 | 随样本量 \(n\) 增大而变窄(更精确) | 相对稳定,不随 \(n\) 增大而明显变窄 |
例题:公式辨析
某指标的均数为 \(\bar{X}\),标准差为 \(S\),由公式 \((\bar{X}-1.96S, \bar{X}+1.96S)\) 计算出来的区间常称为( )。
A. 99%参考值范围
B. 95%参考值范围
C. 99%置信区间
D. 95%置信区间
E. 90%置信区间
正确答案: B
解析: 公式中使用的是标准差 \(S\),这是用于描述个体分布的参考值范围。系数1.96对应95%。
例题:置信区间的含义
95%置信区间的含义为( )。
A. 此区间包含总体参数的概率是95%
B. 此区间包含总体参数的可能性是95%
C. “此区间包含总体参数”这句话可信的程度是95%
D. 此区间包含样本统计量的概率是95%
E. 此区间包含样本统计量的可能性是95%
正确答案: C
解析: 置信区间是随机的,总体参数是固定的。95%是指如果重复抽样100次,平均有95次计算出的区间会包含总体参数,因此解释为“可信程度”最为准确。
统计推断的正确表述
案例辨析:
不能说“点估计值的95%置信区间”,应说“总体均数的95%置信区间”。
不能说“往年均数没落在置信区间内,所以有差异”,应说“置信区间没有覆盖(包括)往年均数,所以差异有统计学意义”。
例题:统计学意义的理解
两样本均数比较,其差别有统计学意义指的是( )。
A. 两总体均数的差别具有实际意义
B. 两样本均数的差别具有实际意义
C. 两样本和两总体均数的差别都具有实际意义
D. 有理由认为两总体均数有差别
E. 有理由认为两样本均数有差别
正确答案: D
解析: 统计推断是由样本推断总体,所以结论必须关于总体(排除E)。统计学意义(显著性)代表差别不是由随机误差造成的,但不代表有实际临床意义(排除A, B, C)。
偏态分布的处理
如果原始数据呈偏态分布,计算参考值范围时不能用正态分布法(\(\bar{X} \pm 1.96S\)),应使用百分位数法。 但是,计算总体均数的置信区间时,如果样本量 \(n\) 足够大,根据中心极限定理,样本均数的分布近似正态,仍可用正态近似法或t分布法计算置信区间。