第2章 概率分布
1. 引言
频率与概率
样本分布的描述:通常使用频率分布表和直方图来描述(第1章内容)。
总体分布的描述:通常使用概率(密度)分布来描述,包括正态分布、二项分布、Poisson分布等。
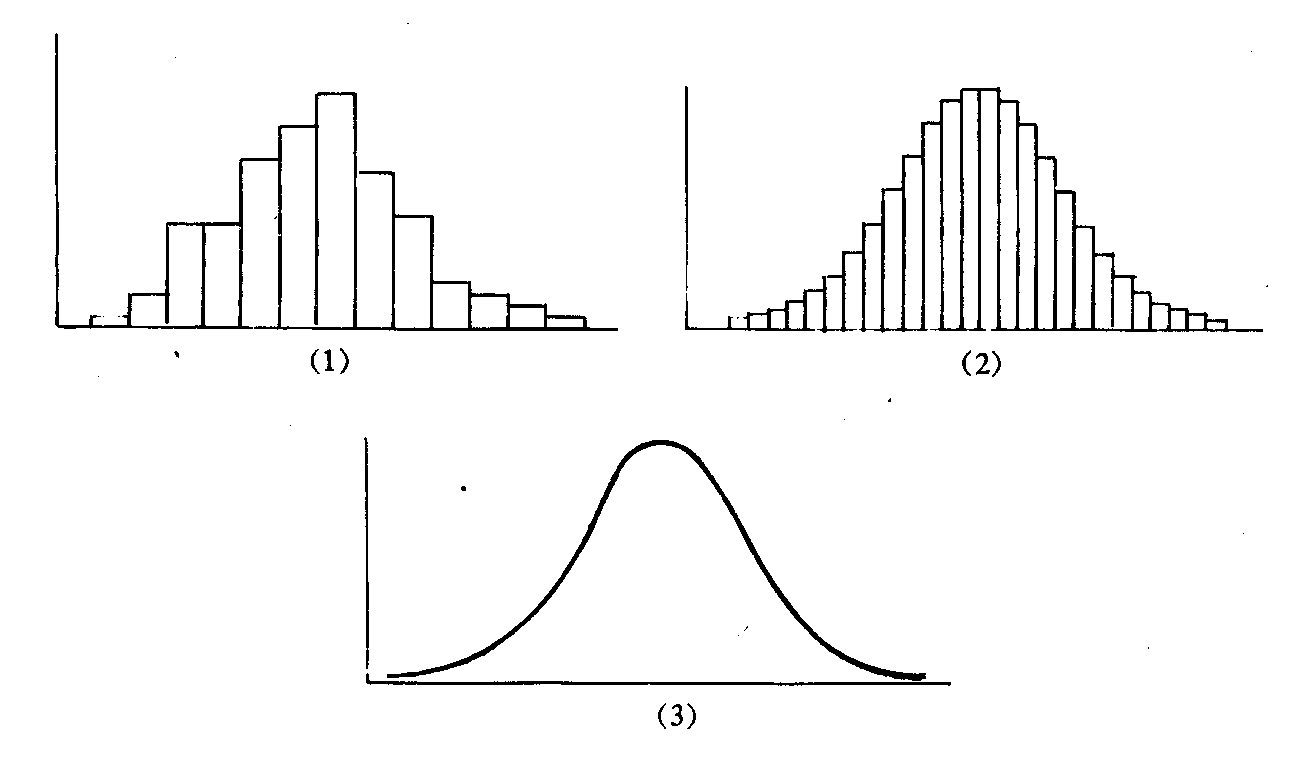
二者关系:随机变量的频率密度直方图近似反映概率密度分布。样本含量越大,频率密度直方图越接近概率密度分布。
2. 正态分布 (Normal Distribution)
概念与特征
定义:正态分布是自然界最常见的一种分布,测量误差、人体的尺寸、医学中的许多检测指标都近似服从正态分布。其概率密度函数(PDF)记作 \(X \sim N(\mu, \sigma^2)\)。
图形特征:
在横坐标上方呈钟型曲线,两端与X轴永不相交,且以 \(X=\mu\) 为对称轴,左右完全对称。
在 \(X=\mu\) 处,\(f(X)\) 取最大值。\(X\) 越远离 \(\mu\),\(f(X)\) 值越小。
两个参数的意义:
位置参数 \(\mu\):决定曲线在X轴上的位置。若固定 \(\sigma\),改变 \(\mu\) 值,曲线沿着X轴平行移动,其形状不变。
形态参数 \(\sigma\):决定曲线的形态。若固定 \(\mu\),\(\sigma\) 越小,曲线越陡峭;\(\sigma\) 越大,曲线越平坦。

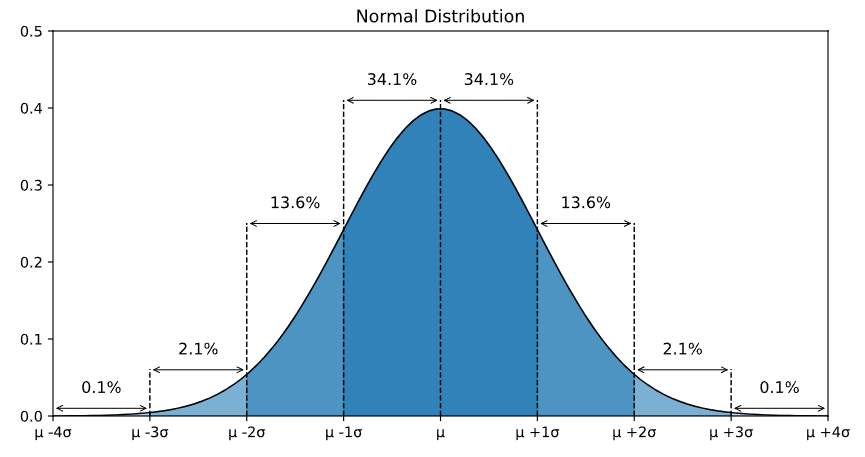
面积分布规律:
X轴与正态曲线所夹面积恒等于1(即100%)。
区间 \(\mu \pm 1\sigma\) 的面积约为 68.2%。
区间 \(\mu \pm 1.96\sigma\) 的面积约为 95%。
区间 \(\mu \pm 2.58\sigma\) 的面积约为 99%。
区间 \(\mu \pm 1.64\sigma\) 的面积约为 90%。
例题:正态分布面积规律
某资料的观察值呈正态分布,理论上有( )的观察值落在 \(\bar{X} \pm 1.96S\) 范围内。
A. 68.27%
B. 90%
C. 95%
D. 99%
E. 45%
正确答案: C
解析: 正态分布中,约95%的观察值落在 \(\bar{X} \pm 1.96S\) 范围内。
例题:正态分布单侧面积
正态曲线下,从均数到+1.64\(\sigma\)的面积为( )。
A. 45%
B. 90%
C. 95%
D. 47.5%
E. 99%
正确答案: A
解析: 正态分布是对称的,\(\mu \pm 1.64\sigma\) 包含90%的面积,因此从均数(中心)到单侧+1.64\(\sigma\)的面积为90%的一半,即45%。
标准正态分布
定义:均数 \(\mu=0\) 且标准差 \(\sigma=1\) 的分布称为标准正态分布,记作 \(N(0,1)\)。
标准化变换:通过变量变换 \(Z = \frac{X-\mu}{\sigma}\),可以将任意正态分布转化为标准正态分布。
累积分布函数 (CDF):表示区间 \((-\infty, x)\) 内的累积概率,即曲线下方的面积。
正态分布变量的性质
正态分布变量之和、之差都仍然服从正态分布。
均数为两者之和或之差:\(E(X_1 \pm X_2) = \mu_1 \pm \mu_2\)。
方差总是两者之和:\(Var(X_1 \pm X_2) = \sigma_1^2 + \sigma_2^2\)。
正态分布的应用
制定医学参考值范围
定义:指包括绝大多数正常人的人体形态、机能和代谢产物等各种生理及生化指标常数,也称正常值。
制定方法
正态分布法(双侧)
适用于正态分布资料。双侧95%参考值范围为 \(\bar{X} \pm 1.96S\)。
因血红蛋白过高、过低均为异常。所以按双侧估计95%医学参考值范围。
百分位数法
适用于任何分布型的资料,特别是偏态分布。双侧95%参考值范围取 \(P_{2.5} \sim P_{97.5}\)。
双侧95%参考值范围:(P2.5, P97.5)如:白细胞数无论过低或过高均属异常
单侧范围:P95以下,如血铅、血清转氨酶仅过高异常 ,或P5以上,如肺活量仅过低异常。
例题:偏态分布参考值制定
在制定医学参考值范围时,若资料呈明显偏态分布,应优先采用哪种方法?
A. 均数±1.96标准差
B. 均数±2.58标准差
C. 百分位数法
D. 几何均数法
E. 中位数±四分位间距
正确答案: C
解析: 百分位数法适用于任何分布,尤其适用于偏态资料;正态分布法仅适用于近似正态分布资料。
例题:对数正态分布参考值
若正常人的血铅含量X近似服从对数正态分布,则制定X的95%参考值范围,最好采用(其中Y=lgX,Sy为Y的标准差)( )。
A. \(\bar{X} \pm 1.96S\)
B. \(P_{2.5} \sim P_{97.5}\)
C. \(lg^{-1}(\bar{Y} + 1.64S_Y)\)
D. \(lg^{-1}(\bar{Y} + 1.96S_Y)\)
E. \(P_5 \sim P_{95}\)
正确答案: C
解析: 血铅含量通常仅过高为异常,故应制定单侧上限(P95)。对于对数正态分布,先取对数转化为正态分布Y,计算单侧95%上限 \(\bar{Y} + 1.64S_Y\),再取反对数还原。
质量控制
原理:如果测量误差仅由随机误差引起,测量数据的波动应服从正态分布。
控制图:利用 \(\bar{X} \pm 3S\) 作为上、下控制限,\(\bar{X} \pm 2S\) 作为上、下警戒限。
统计方法的理论基础
许多统计方法(如t检验、方差分析)要求资料服从正态分布。对属于非正态分布的资料,要先进行变量变换。
有些统计量的分布(如t分布、\(\chi^2\) 分布、F分布等)都是在正态分布的基础上推演出来的。
二项分布和Poisson分布在样本量大时近似正态分布。
3. 二项分布 (Binomial Distribution)
定义与概率
伯努利试验:对于任意一次试验,如果只有事件A发生和不发生两种结果,概率分别为 \(\pi\) 和 \(1-\pi\)。
定义:在相同条件下进行 \(n\) 次独立重复试验,事件发生的次数 \(X\) 服从二项分布,记做 \(X \sim B(n, \pi)\)。
概率公式:\(P(X=k) = C_n^k \pi^k (1-\pi)^{n-k}\)。
分布特征
均数与标准差
总体均数 \(\mu = n\pi\)
总体方差 \(\sigma^2 = n\pi(1-\pi)\)
总体标准差 \(\sigma = \sqrt{n\pi(1-\pi)}\)
图形形状
决定图形的两个参数是 \(n\) 和 \(\pi\)。
当 \(\pi=0.5\) 时,图形对称。
当 \(\pi \ne 0.5\) 且 \(n\) 较小时,图形呈偏态。
中心极限定理
当 \(n\) 较大,且 \(n\pi\) 与 \(n(1-\pi)\) 均大于5时,二项分布接近正态分布。
例题:二项分布的对称性
在样本例数不变的情况下,若( ),则二项分布越接近对称分布。
A. 总体率越大
B. 样本率p越大
C. 总体率越小
D. 总体率越接近0.5
E. 总体率接近0.1或0.5
正确答案: D
解析: 二项分布中,当总体率 \(\pi\) 越接近0.5时,分布越接近对称分布。
应用条件与实例
应用条件:
1.各观察单位仅具有相互对立的两种结果。
2.已知某一结果的概率为 \(\pi\),且固定不变。
3.\(n\)个观察单位的观察结果相互独立。
生物医学应用:例如细胞膜上单离子通道电流的检测(利用二项分布均值和方差的关系进行噪声分析)。
4. 泊松分布 (Poisson Distribution)
定义与特征
定义:描述单位时间、单位面积或单位空间中罕见事件(Rare events)发生数的分布规律。可以看作是二项分布在 \(n \to \infty, \pi \to 0\) 时的极限。
概率公式:\(P(X=k) = \frac{\mu^k}{k!}e^{-\mu}\),记为 \(X \sim \Pi(\mu)\)。
参数特征:
\(\mu\) 是Poisson分布的唯一参数,即总体均数。
总体均数等于总体方差:\(\mu = \sigma^2\)。
例题:Poisson分布参数关系
Poisson 分布的均数 \(\lambda\)(即 \(\mu\))与标准差的关系是( )。
A. \(\lambda = \sigma\)
B. \(\lambda < \sigma\)
C. \(\lambda > \sigma\)
D. \(\lambda = \sqrt{\sigma}\)
E. \(\lambda = \sigma^2\)
正确答案: E
解析: Poisson分布的均数等于方差 (\(\sigma^2\)),即 \(\lambda = \sigma^2\)。
分布图形与可加性
图形:随着 \(\mu\) 增大,分布趋于对称;当 \(\mu \ge 20\) 时,接近正态分布。
可加性:相互独立的Poisson分布变量之和仍服从Poisson分布。
(此处建议插入PPT中“不同均值下的Poisson分布图形”的图片)
例题:血小板计数
某实验室用显微镜计数血小板,每视野平均计数为3个。若要使计数结果近似服从正态分布,应采取什么措施?
A. 减少视野数量
B. 仅计数1个视野
C. 合并多个视野使总均数≥20
D. 使用二项分布建模
E. 改用中位数描述
正确答案: C
解析: Poisson分布在均数 \(\mu \ge 20\) 时近似正态分布。通过合并相互独立的观察单位(如多个视野),可以提高总均数,使其满足正态近似条件。
应用场景
Poisson分布常用于描述稀有事件的发生次数。例如:
1.放射性物质单位时间内的放射次数。
2.单位体积内粉尘或细菌的计数。
3.人群中患病率很低的非传染性疾病的患病数。
例题:稀有事件分布
铅作业工人周围血点彩红细胞在血片上的出现数近似服从( )。
A. 二项分布
B. 正态分布
C. 偏态分布
D. Poisson 分布
E. 对称分布
正确答案: D
解析: 铅作业工人血点彩红细胞出现数属于稀有事件(发生概率极低),近似服从Poisson分布。