第1章 统计描述
1. 概述
统计分析的组成
统计分析主要包含两个部分
统计描述:利用统计指标和统计图表描述样本资料的分布规律及其数量特征。
统计推断:利用样本信息推断总体特征。
本章重点在于如何从数据中提取信息,通过指标和图表进行表达。
2. 定量资料的统计描述
定量资料的描述主要通过频率表、直方图以及各类统计指标来进行。
频率表与直方图
频率表用于考察资料的分布形状。制作步骤包括求全距、确定组距、划分组段、统计频数。
频率表
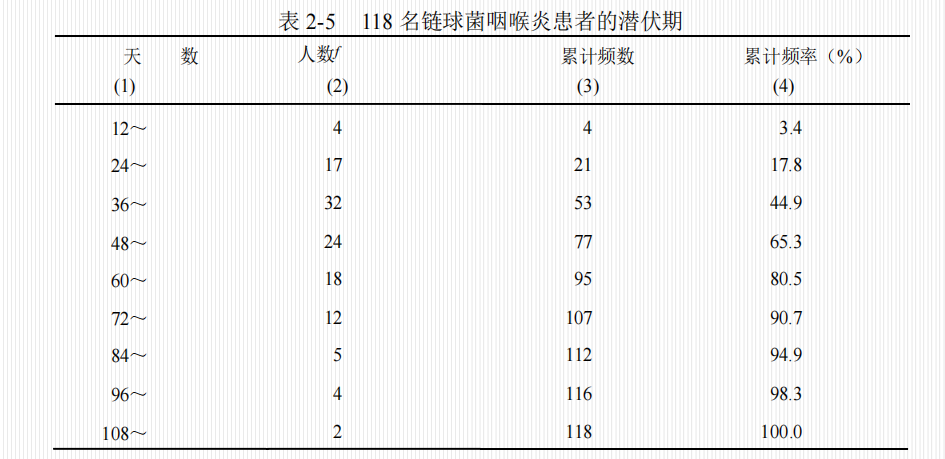
直方图
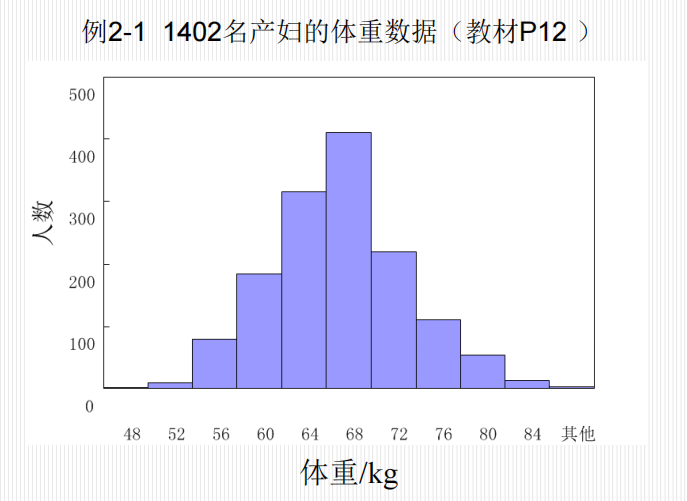
直方图的3种纵坐标
频数(组距中的个体数)
频率(个体数/总体数,即百分比)
频率密度(频率/组距)
组段的划分原则
组段通常取10-15组。
组段必须连续且不重叠。
通常采用“左闭右开”区间(\(L \le X < U\))或特定精度下的互斥区间。
例题:频率表的编制
编制频数表时错误的作法是( )。
A. 用最大值减去最小值求全距
B. 组距常取等组距,一般分为10~15组
C. 第一个组段须包括最小值
D. 最后一个组段须包括最大值
E. 写组段,如“1.5~3,3~5,5~6.5,…”
正确答案: E
解析: 编制频数表时,组段应连续且不重叠,通常采用“下限≤x<上限”的形式(如“1.5~<3.0”)。选项E中“3”同时出现在两个组段(“1.5~3”和“3~5”),造成边界重复,易引起归类混乱。
用途
(1)考察资料的分布特性和类型
如:对称分布、偏峰分布
(2)描述频数分布的特征量
如:变异范围(全距)、数据集中的部位等
(3)便于发现一些特大或特小的可疑值
(4)便于进一步做统计分析和处理
统计描述指标

集中趋势指标 (Average Level)
描述一组变量值的集中位置或平均水平。
算术均数 (Arithmetic Mean)
定义:所有观察值之和除以观察值个数,符号为 \(\bar{X}\)(样本)或 \(\mu\)(总体)。
适用条件:单峰对称分布,特别是正态分布资料。
几何均数 (Geometric Mean)
定义:n个变量值乘积的n次方根,符号为 \(G\)。
适用条件:等比级数资料,或经对数转换后呈对称分布的资料(如抗体滴度、细菌计数等)。
例题:几何均数的应用
以下哪种资料最适合用几何均数描述其平均水平?
A. 某地100名新生儿的出生体重(kg)
B. 某班级学生期末考试成绩
C. 某人群血清抗体滴度数据
D. 住院天数(天)
E. 某地区每日门诊量
正确答案: C
解析: 几何均数适用于等比资料或对数转换后呈对称分布的资料,如抗体滴度、细菌浓度等。
中位数 (Median)
定义:将一组数值从小到大排列后,位次居中的数值,符号为 \(M\)。
特点:不受极端值影响。
适用条件:偏态分布资料、一端或两端无确切数值(开口资料)、分布类型不明的资料。
例题:偏态分布的描述
描述一组负偏峰分布资料的平均水平时,适宜的统计量是( )。
A. 中位数
B. 几何均数
C. 调和均数
D. 算术均数
E. 众数
正确答案: A
解析: 负偏峰(左偏)分布中,数据左侧有长尾,算术均数受极端小值影响而小于中位数,此时中位数更能代表集中趋势,不受极端值干扰。
百分位数 (Percentile)
定义:将数据分为两部分,\(P_X\) 表示有 \(X\%\) 的变量值比它小。
常用指标:\(P_{50}\) 即中位数;\(P_{25}\) 为下四分位数;\(P_{75}\) 为上四分位数。
离中趋势指标 (Variation)
描述变量值的变异程度或离散水平。
全距 (Range)
定义:最大值与最小值之差 (\(R = Max - Min\))。
缺点:仅利用了两个极端值的信息,不稳定。
四分位数间距 (IQR)
定义:上四分位数与下四分位数之差 (\(IQR = P_{75} - P_{25}\))。
意义:反映了中间50%数据的变异程度,比全距稳定。
适用:偏态分布资料。
例题:IQR的定义
关于四分位数间距(IQR),下列说法正确的是?
A. IQR = P90 – P10
B. IQR受极端值影响较大
C. IQR适用于描述对称分布资料的离散程度
D. IQR = P75 – P25,反映中间50%数据的变异
E. IQR的单位与原始数据不同
正确答案: D
方差 (Variance) 与标准差 (Standard Deviation)
方差:也称均方差,反映数据平均离散水平。
标准差 (S):方差的算术平方根,具有与原始数据相同的量纲。
意义:S 越小,说明数据越集中于均数附近,均数的代表性越好。
适用:正态分布或近似正态分布资料。
例题:均数与标准差的关系
均数和标准差S的关系是( )。
A. S越小,对样本中其他个体的代表性越好
B. S越大,对样本中其他个体的代表性越好
C. 均数越小,S越大
D. 均数越大,S越小
E. 均数必小于S
正确答案: A
解析: 标准差S反映数据围绕均数的离散程度。S越小,说明数据越集中于均数附近,均数对样本中其他个体的代表性越好。
变异系数 (Coefficient of Variation, CV)
定义:标准差与均数之比 (\(CV = S/\bar{X} \times 100\%\))。
特点:无量纲。
适用条件:
比较不同量纲(单位)变量的变异程度(如身高 vs 体重)。
比较均数相差较大的同一指标的变异程度(如儿童身高 vs 成人身高)。
例题:变异程度的比较
比较5年级小学生瞳距和他们坐高的变异程度,宜采用( )。
A. 变异系数
B. 全距
C. 标准差
D. 四分位数间距
E. 百分位数P2.5与P97.5的间距
正确答案: A
解析: 瞳距与坐高单位相同但均值差异较大,或者即使单位不同,比较不同量纲或均值相差较大的变量的变异程度时,应使用无量纲的变异系数。
例题:标准差与CV的区别
标准差与变异系数的主要区别在于?
A. 标准差有单位,变异系数无单位
B. 标准差适用于偏态分布,变异系数适用于正态分布
C. 变异系数总是小于标准差
D. 标准差可用于定性资料,变异系数不能
E. 两者计算方法完全相同
正确答案: A
解析: 变异系数是标准差与均数之比,消除了量纲。
例题:离中趋势指标汇总
以下表示离中趋势的是:
A. 全距
B. 四分位数间距
C. 方差
D. 标准差
E. 变异系数
正确答案: A B C D E
分布趋势指标
偏度 (Skewness)
描述分布不对称的方向和程度。数据相对于平均值的不对称变化程度
正偏态 (Positive Skew):长尾向右(大数值方向),Mean > Median。
负偏态 (Negative Skew):长尾向左(小数值方向),Mean < Median。
正态分布:偏度 = 0。
公式:\(\frac{m_3}{s^3}\),\(m_3\)为三阶中心矩
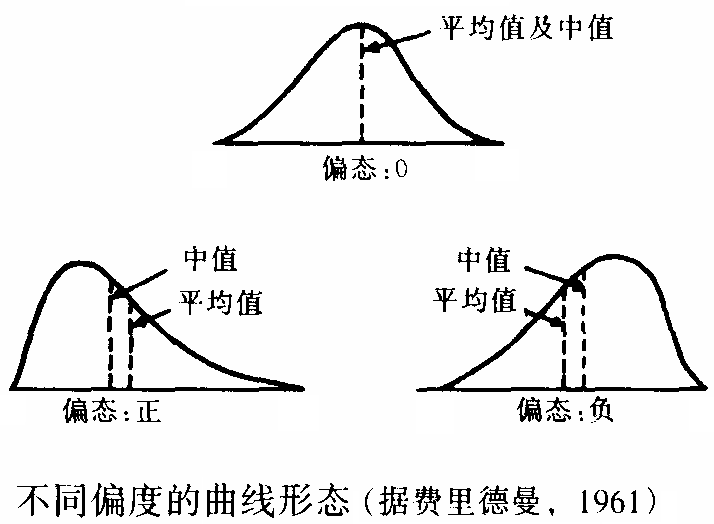
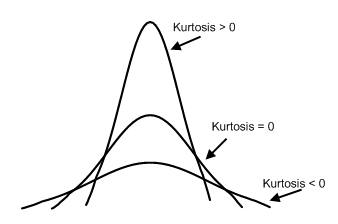
峰度 (Kurtosis)
描述分布的陡峭或平坦程度。数据分布高耸程度的衡量指标
正态分布:峰度 = 3 (或 0,取决于算法定义)。
公式:\(\frac{m_4}{s^4}\),\(m_4\)为四阶中心矩
3. 定性资料的统计描述
定性资料主要使用相对数指标进行描述。
常用相对数指标
频率 (Frequency)
定义:表示某一事件的发生率(如发病率、死亡率)。
公式:\(\frac{\text{某事件发生的个体数}}{\text{可能发生某事件的个体总数}} \times K\)。
特点:分子是分母的一部分,无量纲,取值 0-1。
例题:频率的计算
计算乙肝疫苗接种后血清抗-HBs的阳转率,分母为( )。
A. 阳转人数
B. 疫苗接种人数
C. 乙肝患者数
D. 乙肝病毒携带者数
E. 易感人数
正确答案: B
解析: 阳转率 =(接种后抗体阳转人数 / 接种疫苗总人数)×100%,分母应为实际接受疫苗接种的人数。
强度 (Intensity)
定义:单位时段内某事件的发生率,常带有时间单位(如人年)。
公式:\(\frac{\text{某事件发生的个体数}}{\sum(\text{可能发生该事件的个体总数} \times \text{时间})} \times K\)。
适用:大人群长时间随访资料,分母为“人时”或“人年”。
例题:强度指标的判断
某医院的院内感染率为5.2人/千人日,则这个相对数指标属于( )。
A. 频率
B. 频率分布
C. 强度
D. 相对比
E. 算术均数
正确答案: C
解析: 强度相对数表示单位时间、单位人群或单位暴露下的事件发生频率,具有“率”的性质,常带有时间或暴露单位(如人/千人日)。
相对比 (Relative Ratio)
定义:两个相关联的变量 A 与 B 之比 (\(A/B\))。
特点:A 与 B 互不包含,量纲可以不同。
例子:性别比、变异系数、相对危险度(RR)、比值比(OR)。
应用相对数的注意事项
使用相对数时需严谨,避免误用。
概念混淆:需区分频率、强度和相对比。
分母过小:样本量太小时,相对数波动大,宜直接用绝对数。
率的合并:观察单位数不等的几个率,不能直接相加求平均,应遵循“分子之和除以分母之和”的原则。
可比性:比较时需注意内部构成(如年龄结构)的影响,必要时进行标准化处理。
例题:相对数应用注意事项
应用相对数指标时,应该注意的是(可能出大题):
A. 防止概念混淆,相对数的计算是两部分观察结果的比值,根据这两部分观察结果的特点,就可以判断所计算的相对数属于频率,强度,还是相对比等
B. 计算相对数时分母不宜过小,样本量较小时以直接报告绝对数为宜。
C. 观察单位数不等的几个相对数,不能直接相加求其平均水平。
D. 相对数间的比较须注意可比性,有时需分组讨论或计算标准化率。
正确答案: A B C D
4. 统计图表的制作
统计表 (Statistical Table)
三线表:主要由顶线、底线、分隔线(纵标目下)组成。

制表原则:
重点突出,一张表表达一个主题。
简单明了,不留空格,无数字用“—”表示,缺失用“…”表示。
注释放在表下方。
统计图 (Statistical Chart)
用几何图形形象化表达数据。

常用图形及其适用范围
| 图形 | 适用资料 | 特点/注意事项 |
|---|---|---|
| 条图 (Bar Chart) | 组间数量对比 | 直条高度表示数量大小,纵轴必须从0开始。 |
| 百分条图/饼图 | 构成比(频率分布) | 面积或角度表示比例。 |
| 直方图 (Histogram) | 定量变量的频率分布 | 面积表示频率,直条间无间隙。 |
| 线图 (Line Chart) | 变量随时间或有序指标的变化 | 需用算术尺度坐标。 |
| 散点图 (Scatter Plot) | 双变量间的相关关系 | |
| 箱式图 (Box Plot) | 定量变量的分布特征 | 箱式图用5个统计量反映数据的分布特性。展示5个统计量(Min, \(P_{25}\), \(P_{50}\), \(P_{75}\), Max),纵轴可不从0开始。 |
例题:统计图坐标轴设置
纵坐标可以不从0开始的图形为( )。
A. 直方图
B. 单式条图
C. 复式条图
D. 箱式图
E. 以上均不可
正确答案: D
解析: 直方图、条图等用于表示绝对数量或频率的图形,纵轴必须从0开始,否则会误导视觉;而箱式图展示的是数据的分布特征(如中位数、四分位数、异常值),其纵轴反映的是数据的实际取值范围,可不从0开始。