第0章 绪论
1. 统计学的定义与意义
什么是统计学
统计学是一门关于数据的科学。它处理大量数据的收集、分析、解释和表达,目的是从不确定性中寻找确定性。
描述统计
总结数据的特征(如计算平均值、制表绘图)。
推断统计
利用样本数据推断总体特征(如假设检验、参数估计)。
统计工作的全过程
科研工作中的统计学应用贯穿全过程,包含以下四个关键步骤:
科研选题与设计(决定数据质量的关键)
实验与测量(数据采集)
数据分析
结论与报告
2. 核心基本概念
变量及其类型
根据数据的性质,变量主要分为两大类:定量变量和定性变量。
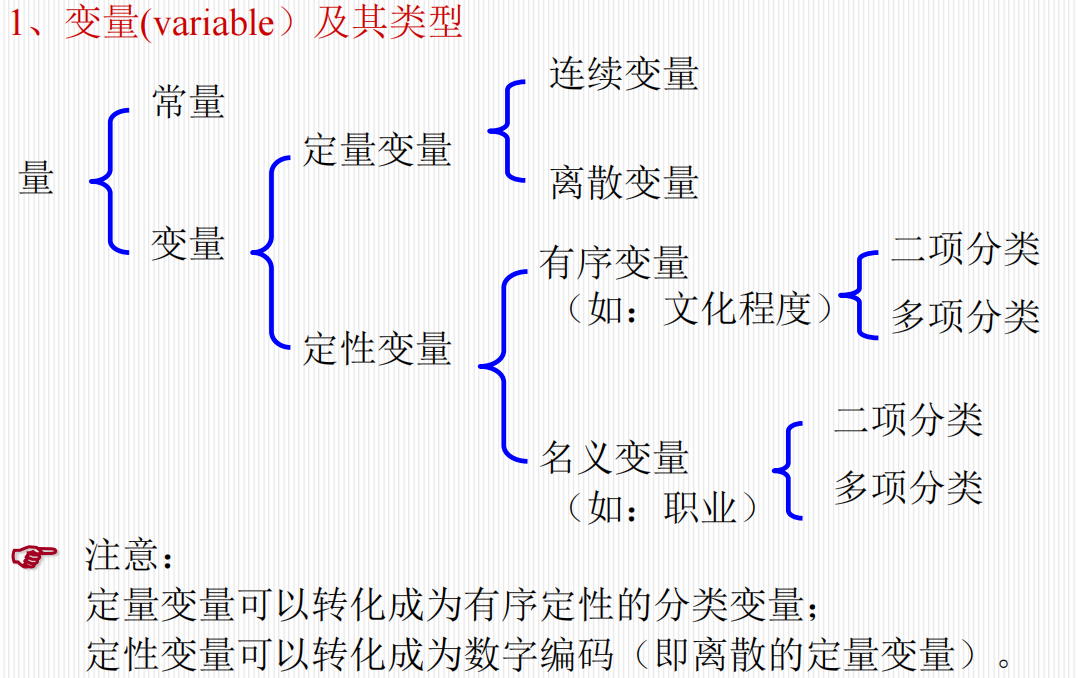
定量变量
数值变量,表现为数值的大小,可以进行数学运算。
连续型变量
可以取数轴上任意值(如:身高、体重、血压)。
离散型变量
只能取整数值(如:红细胞计数、脉搏次数)。
定性变量
分类变量,表现为互不相容的类别或属性。
名义变量 (Nominal)
类别之间互不相容,无等级顺序关系。
例如:性别(男/女)、血型(A/B/O/AB)、职业。
有序变量 (Ordinal)
类别之间有等级顺序关系(强弱、大小、深浅)。
例如:疗效(痊愈 > 显效 > 有效 > 无效)、病情分级(轻/中/重)、尿蛋白(- / + / ++)。
注意: 变量类型不是绝对的,定量变量可以转化为有序变量(如按年龄分段),定性变量也可以编码为数字(但需注意其数学意义)。
例题:有序分类变量
在生物医学研究中,将“疗效”分为“痊愈、显效、有效、无效”四个等级,该变量属于?
A. 是连续型定量变量
B. 是离散型定量变量
C. 是名义变量
D. 是有序分类变量
E. 非常适合使用平均数±标准差来描述
正确答案: D
解析: 看到“等级”、“程度”、“分级”等字眼,且类别之间有强弱顺序(痊愈 > 显效 > 有效 > 无效),必选有序分类变量。
例题:名义变量
下列资料属名义变量的是?
A. 白细胞计数
B. 住院天数
C. 门急诊就诊人数
D. 患者的病情分级
E. ABO血型
正确答案: E
解析: A、B、C是定量变量;D是有序变量(有轻重之分);E(A/B/O/AB型)是纯粹的分类,无高低之分,故为名义变量。
同质与变异
同质
根据研究目的,要求研究对象在主要研究因素以外的其他因素尽可能相同(如:都是2025年杭州市7岁男童)。
变异
在同质基础上个体之间的差异(如:即使是双胞胎,身高体重也有差异)。
结论: 没有变异就没有统计学。统计学就是研究如何在变异的数据中寻找规律。
例题:概念辨析
下列关于“同质”与“变异”的说法中,正确的是?
A. 同质意味着研究对象在所有方面完全相同
B. 变异是指研究对象之间不存在任何差异
C. 统计学研究的前提是存在变异,而变异必须建立在同质基础上
D. 同质与变异是相互排斥的概念
E. 只有在实验研究中才需要考虑同质性
正确答案: C
解析: 统计学就是研究如何在“变异”的数据中寻找规律的科学,而“同质”是进行比较的前提。
总体、样本与观察单位
观察单位
也称个体,个体是研究的基本单位。
总体
根据研究目的确定的同质研究对象的全体。分为有限总体和无限总体。
样本
从总体中随机抽取的一部分个体。
抽样的核心目的
我们无法测量无限总体,只能通过抽取样本,利用样本统计量来推断总体参数。
例题:基本单位
研究中的基本单位是指?
A. 样本
B. 全部对象
C. 影响因素
D. 个体
E. 总体
正确答案: D
例题:抽样目的
从总体中抽取样本的目的是?
A. 研究样本统计量
B. 由样本统计量推断总体参数
C. 研究典型案例
D. 研究总体统计量
E. 计算统计指标
正确答案: B
解析: 这是统计推断(Inferential Statistics)的核心定义。
参数与统计量
| 维度 | 参数 | 统计量 |
|---|---|---|
| 描述对象 | 总体 | 样本 |
| 性质 | 常量 (固定值,通常未知) | 随机变量 (随抽样不同而波动) |
| 符号表示 | \(\mu, \sigma, \pi\) | \(\bar{X}, S, p\) |
| 获取方式 | 理论值或普查获得 | 由样本数据计算得出 |
例题:概念辨析
关于参数与统计量,下列说法正确的是?
A. 参数是根据样本计算得出的
B. 统计量是描述总体特征的固定值
C. 参数通常用英文字母表示,如X̄
D. 统计量是随机变量,会随样本不同而变化
E. 总体参数可以通过一次抽样精确获得
正确答案: D
解析: A错(参数是总体的);B错(统计量描述样本且不固定);C错(参数用希腊字母);E错(抽样只能推断,不能精确获得参数,除非普查)。
例题:参数定义
参数是指?
A. 参与个体数
B. 描述总体特征的统计指标
C. 描述样本特征的统计指标
D. 样本的总和
E. 参与变量数
正确答案: B
误差
实测值与真实值之差,主要分为两类。
随机误差
原因: 由个体变异性引起,偶然因素导致。
特点: 无方向性(双侧性)、不可避免、有统计规律(服从正态分布)。
控制: 增加样本含量(重复测量)可以减小,但不能消除。
系统误差
原因: 仪器未校准、试剂不纯、抽样不均匀(偏倚)。
特点: 有方向性(单侧偏差,总是偏大或偏小)、理论上可以消除。
控制: 必须通过改进实验设计、校准仪器来消除。重复测量不能减小系统误差。
注: 实验中的人为读数错误属于过失误差,必须杜绝,不属于统计学误差的范畴。
例题:随机误差
关于随机误差下列不正确的是?
A. 受测量精密度限制
B. 无方向性
C. 也称为偏倚
D. 不可避免
E. 增加样本含量可降低其大小
正确答案: C
解析: “偏倚”通常特指系统误差。随机误差是不可避免的偶然波动。
例题:系统误差
下列关于系统误差的说法,错误的是?
A. 系统误差具有方向性(单侧偏差)
B. 系统误差可能由仪器未校准引起
C. 重复测量可有效减小系统误差
D. 系统误差属于可避免的误差类型
E. 某研究者调查某高校学生熬夜习惯,仅在某学院晚自习教室发放问卷,则该结果最可能受到系统误差影响
正确答案: C
解析: 重复测量(增加样本量)只能平抑随机波动(随机误差),如果仪器本身是歪的(系统误差),测一万次也是歪的。
频率与概率
概率 (P)
随机事件发生可能性的度量。
取值范围:\(0 \le P \le 1\)。
\(P=1\) 为必然事件,\(P=0\) 为不可能事件。
频率
样本中某事件发生的比例。用于估计总体的概率。
小概率事件
定义:\(P \le 0.05\) 或 \(P \le 0.01\) 的事件。
意义:统计学认为小概率事件在一次试验中基本不可能发生。这是假设检验推断的理论依据。
3. 常见统计误区案例
在实际应用中,必须注意统计方法的适用条件。
案例1:算术平均值的适用条件
错误: 数据分布不均匀(如双峰、严重偏态)时直接求均值。
正确: 算术平均值适用于正态分布或近似正态分布的定量资料。偏态分布应用中位数描述。
案例2:观察单位不等的平均数计算
错误: 将几个不同组的率(如工作效率)直接相加求平均。
正确: 应遵循分子相加、分母相加的原则,重新计算总率。
案例3:“平均数±标准差”的滥用
错误: 对明显偏态分布(标准差 > 平均数,或包含负值逻辑不可能)的数据使用 \(\bar{X} \pm S\)。
正确: \(\bar{X} \pm S\) 仅适用于正态分布资料描述集中和离散趋势。
案例4:圆分布资料
错误: 对时间点(如22点、2点)、角度等首尾相接的数据直接算术平均(例如认为22点和2点的平均是12点,这是错误的)。
正确: 使用圆分布资料统计法,转换为角度计算。
例题:圆分布资料
在分析某地区24小时内急诊就诊人数的时间分布时,若直接计算小时数的算术平均值(如23点、0点、1点的平均为8点),会导致错误结论。此时应采用哪种统计方法?
A. 使用中位数代替均数
B. 使用百分位数描述
C. 采用圆分布资料统计法
D. 进行方差分析
E. 使用卡方检验
正确答案: C
解析: 凡是涉及“钟表时间”、“角度”、“季节周期”等首尾相接的数据,均需使用圆分布法。
案例5:统计图绘制假象
错误: 两个坐标刻度不等长、间隔不一致,导致曲线趋势产生视觉误导。
正确: 坐标轴刻度必须均匀等长。
案例6:样本与总体的混淆
错误: 误将“发病人员中性别的比例”当作“人群中该性别的发病率”。
例子: 病人中95%是男性,不能说明男性更容易得病(因为可能总人群中男性本来就多)。
正确: 计算发病率的分母应该是该群体的总人数,而不是病例数。
案例7:小样本结论
错误: 样本量太小(如n=5)时,仅凭直观数据大小得出“A优于B”的结论。
正确: 必须进行假设检验(如利用样本推断总体),并给出统计学结论。
4. 科研设计的基本原则
研究设计应遵循四个基本原则,目的是控制随机误差,避免系统误差。
随机化
目的:保证样本代表性,使非处理因素在各组间分布均衡。
方法:随机抽样、随机分组。
对照
目的:排除非处理因素的干扰,鉴别处理因素的效应。
类型:空白对照、实验对照、标准对照、自身对照等。
重复
目的:估计实验误差,提高结果的可靠性。
要求:要有足够的样本含量。较小动物 \(\ge 10\) 只。较大动物 \(\ge 5\) 只。
均衡
目的:各组之间除处理因素外,其他条件尽可能一致(同质性)。