第6章 离散时间信号和系统的频域分析

1.离散时间信号傅里叶变换 DTFT

采用采样的思想

\(x(t)\rightarrow x(nT)=x[n]\) $$ X(\omega T)=\sum_{n=-\infty}^{+\infty}x(nT)e^{-j\omega nT} $$ 令\(\omega T=\Omega\)​， $$ X(\Omega)=\sum_{n=-\infty}^{+\infty}x[n]e^{-j\Omega n} $$ \(\Omega=\frac{\omega}{\omega_s}\cdot 2\pi\)，将\(\Omega\)​叫作归一化数字角频率

傅里叶反变换

\[ x[n]=\int_{0}^{2\pi}X(\Omega)e^{j\Omega n}d\Omega \]

存在条件

\[ \sum_{n=-\infty}^{+\infty}|x[n]|<\infty \]

一个有限长序列，它的傅里叶变换一定存在

\(X(\Omega)\)周期性

\[ X(\Omega+2\pi)=X(\Omega) \]

从采样角度看，由于\(X_s(\omega)\)是\(X(\omega)\)的复制搬移，而\(X(\Omega)\)和\(X_s(\omega)\)相比只是对横坐标做了一个归一化处理，所以必然是周期的，且周期为\(2\pi\)

\(e^{-an}u[n]\)DTFT

\[ e^{-an}u[n]\leftrightarrow \frac{1}{1+e^{-a}e^{-j\Omega}} \]

若要计算幅值，把\(e^{-j\Omega}\)用欧拉公式展开

一些广义DTFT

DTFT的性质

DTFT的高频和低频

将任意\(x(t)\)以\(\omega_s\) 的采样角频率采样后，频谱中最高频率理论上为\(\frac{\omega_s}{2}\)

对应的\(\Omega\)​值又为π

以\((-\pi,\pi)\)为例，\(|\Omega|\)越接近\(\pi\)，为高频；\(|\Omega|\)越接近0，为低频

低通/高通/带通滤波器的判断

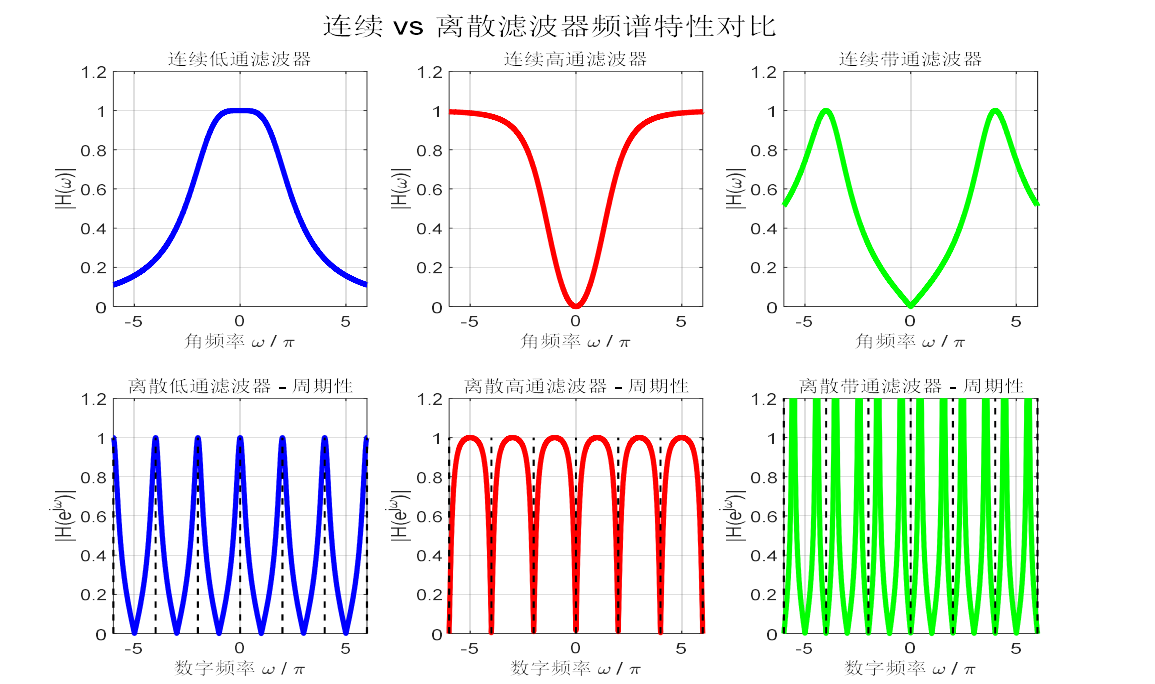
判断DTFT的滤波器，主要看\((-\pi,\pi)\)的区域，若为\((0,2\pi)\)，建议将\((\pi,2\pi)\)的段对称到\((-\pi,0)\)

2.离散傅里叶变换 DFT

DTFT无法在工程上被分析，连续的频域也无法被计算机处理，用DFT来离散化DTFT来观测DTFT

前提条件：\(x[n]\)有限长，\(l\le N\)

\(\Omega=\frac{2\pi}{N}k\)，\(k\)为频域的离散值 $$ X_k=\sum_{n=0}^{N-1}x[n]e^{\frac{-j2\pi}{N}k} $$